Mathematische Modelle ermöglichen es, komplexe Körper, Flächen, Kurven oder Funktionen visuell und haptisch fassbar zu machen. Als Hilfsmittel kamen sie – und kommen bisweilen noch – zur Vermittlung geometrischer Kenntnisse in schulischer und universitärer Mathematik zum Einsatz. Teilweise übernahmen sie auch in natur- und technikwissenschaftlichen Disziplinen, in denen angewandtes geometrisches Wissen wichtig war, didaktische Funktionen. Selbst wenn das moderne Paradigma einer formalisierten, der Visualisierung tendenziell abgeneigten Mathematik ihren Erkenntniswert in Abrede zu stellen schien: Als Medien der Kommunikation mathematischer Praxis und als historische Sachzeugen sind die Modelle nicht aus den Universitäten verschwunden. Davon zeugen die hier versammelten Bestände, deren Entstehungszeiträume vom 19. Jahrhundert bis in die Gegenwart hineinreichen.
Die Geschichte mathematischer Modelle ließe sich bis zur Beschäftigung mit Archimedischen und Platonischen Körpern im antiken Griechenland zurückverfolgen. An deutschen Universitäten tauchen sie spätestens im 18. Jahrhundert auf: So sollen bereits zu Zeiten Abraham Gotthelf Kästners an der Universität Göttingen Kartonmodelle zur Visualisierung komplexer Polyeder genutzt worden sein (Burmann/Krämer/Patterson 2001, 175). Ihre Blütezeit erlebten die Objekte aber im letzten Drittel des 19. Jahrhunderts, als man sich an vielen Hochschulen in der mathematischen Ausbildung um Anschaulichkeit bemühte. Wichtige Befürworter der Praxis des Modellierens waren Felix Klein und Alexander von Brill, die unter anderem zum Aufbau von Sammlungen in München, Tübingen und Leipzig beitrugen. Brill betonte 1886 das produktive, erkenntnisfördernde Potential der Modelle: „Die Mannigfaltigkeit dieser Formen regt [...] die Einbildungskraft an, und der öftere Umgang mit ihnen zieht auch den mit räumlicher Anschauung wenig Begabten zum Interesse an der Geometrie heran und reizt den Talentvolleren zum Vergleichen und Nachdenken“ (Brill 1886, 70). Zum Nachdenken und Vergleichen, insofern als heuristisches Mittel, nutzte auch Felix Klein die Objekte in seinen Forschungen über algebraische Flächen und verfocht die Bedeutung räumlicher Anschauung auf theoretischer Ebene (Mehrtens 2004, 288f.). Bisweilen wurden auf Bestreben Kleins, Brills und ihrer Schüler, darunter Walther von Dyck, ganze Modellierkabinette eingerichtet. Der Modellbau sollte konstitutiver Teil schulischer und universitärer Lehrpläne werden – was zumindest an technischen Akademien teilweise gelang. In dieser Hochphase nahm auch die Fabrikation durch kommerzielle Hersteller zu, um den Materialbedarf zu decken. Ein Unternehmen wie der von Ludwig Brill gegründete Modellverlag (später Verlagshandlung Martin Schilling), der unter anderem die mathematischen Institute in Halle und Heidelberg belieferte, konnte in dieser Situation prosperieren.
Nach dem Ersten Weltkrieg ebbte das Interesse an mathematischen Modellen jedoch nach und nach ab. Zu den didaktischen und ökonomischen Gründen ihres langsamen Verschwindens trat auch ein theoretischer Diskurs, der den Nutzen von Visualisierungsversuchen in der Mathematik in Zweifel zog: Nicht wenige Vertreter der modernen Mathematik, die tendenziell auf Allgemeinheit und Abstraktion zielte, standen dem Konzept der Anschauung in Kantscher Tradition skeptisch gegenüber. Moderne axiomatische Geometrie, wie sie unter anderem David Hilbert ab den späten 1890er Jahren vertrat, griff lediglich noch zur Illustration oder Kommunikation mathematischer Sachverhalte auf Modelle zurück (Mehrtens 2004, 299). Als Hans Hahn 1933 die “Krise der Anschauung” konstatierte, waren die noch vorhandenen Objekte bereits kaum mehr im Einsatz – bestenfalls wurden sie noch auf den Fluren der Institute ausgestellt. Der Vergleich mit dem Schicksal anderer Materialbestände an Universitäten legt nahe, dass viele der mathematischen Modellsammlungen aus der Blütezeit des späten 19. Jahrhunderts vor allem aufgrund ihrer ästhetischen Qualitäten der Auflösung entgingen. Nicht grundlos traten sie auch in der modernen und zeitgenössischen Kunst wiederholt als Motive und Ausstellungsobjekte in Erscheinung.
In den Wissenschaften erlebten die Techniken des Modellierens nach dem Zweiten Weltkrieg punktuelle Renaissancen. An manchen Orten, wie in Berlin, Bochum oder Dresden, wurden neue Modellsammlungen angelegt, deren Bestände sich aus Restposten alter Modelle, aber auch neuen Modellen aus der Produktion des Berliner Lehrmittelherstellers Rudolf Stoll KG zusammensetzten.
Seitdem wurden die Objekte nach und nach rehabilitiert: In den universitären Unterricht fanden sie als Hilfsmittel zunehmend zurück, und neue technische Möglichkeiten der EDV von Computergrafik bis 3D-Druck ließen nicht nur ein Interesse an virtuellen, sondern auch an materiellen mathematischen Modellen wieder aufleben. So sind beispielsweise an der TU Dresden neue dreidimensionale Objekte hergestellt worden, und Ausstellungen wie an der Universität Halle-Wittenberg im Jahr 2008 präsentieren die Modelle einer interessierten Öffentlichkeit. Wer sich den Objekten aus wissenschaftsgeschichtlicher, aus didaktischer oder aus künstlerischer Perspektive nähern will, findet in dieser Datenbank einen Zugang zu alten und neuen Materialbeständen.

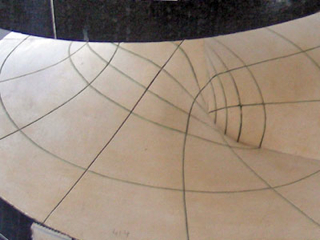
![Modell von Ringzykliden mit Schnittkurven von doppelt berührenden Ebenen [Schilling IX, 8 / 87]](/img/vtfmdx/Mathe1_mdx287.jpg)
![Modell einer Algebraischen Fläche [Stoll 603/63]](/img/vtfmdx/Mathe2_mdx244.jpg)